RAZÕES TRIGONOMÉTRICAS


INTRODUÇÃO

A trigonometria no triângulo retângulo é o estudo sobre os triângulos que possuem um ângulo interno de 90°, que são os triângulos de ângulo reto.

O triângulo retângulo é formado:

• Catetos: são os lados do triângulo que formam o ângulo reto. São classificados em: cateto adjacente e cateto oposto. 
• Hipotenusa: é o lado oposto ao ângulo reto, sendo considerado o maior lado do triângulo retângulo. 

RELAÇÕES TRIGONOMÉTRICAS



INTRODUÇÃO

As relações trigonométricas são relações entre valores das funções trigonométricas de um mesmo arco, também chamadas de identidades trigonométricas.

Inicialmente a trigonometria tinha como objetivo o cálculo das medidas dos lados e ângulos dos triângulos.

Nesse contexto, as razões trigonométricas sen θ, cos θ e tg θ são definidas como relações entre os lados de um triângulo retângulo.

Dado um triângulo retângulo ABC com um ângulo agudo θ, conforme figura abaixo:

A partir da imagem acima, definimos as razões trigonométricas seno, cosseno e tangente em relação ao ângulo θ, como:

Sendo,

a: hipotenusa, ou seja, lado oposto ao ângulo de 90º.

b: cateto oposto ao ângulo θ.

c: cateto adjacente ao ângulo θ. 

Relações Trigonométricas do Triângulo Retângulo

As relações trigonométricas são resultado da divisão entre as medidas de dois lados de um triângulo retângulo, e por isso são chamadas de razões.

Temos então:

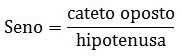
*cateto oposto sobre a hipotenusa.

*cateto adjacente sobre a hipotenusa.

*cateto oposto sobre o cateto adjacente.

A tabela trigonométrica apresenta os valores dos ângulos agudos (menores que 90°) das relações trigonométricas: seno, cosseno e tangente. Esses valores facilitam os cálculos que envolvem a trigonometria no triângulo retângulo.

Além delas, temos as razões inversas: secante, cossecante e cotangente.

* um sobre o cosseno.

* um sobre o seno.

* cosseno sobre o seno.